精度保証付き数値計算とは?

シミュレーションは，日本語で模擬実験を意味し，ある現象に対して何かしらの法則を導き出し(モデリング)，導き出した法則に従って問題を解く(数値計算)ことによって模擬的に知りたい情報を予測する技術です. 問題を解く際に利用される数値計算は現代の発達したコンピュータを利用しますが，残念ながら，コンピュータといえども，完全に解くことは困難です. 例えば，円周率を考えても，円周率は無理数であるため無限の桁を必要とします. 無限の桁をコンピュータで扱うには，無限のメモリーや計算を必要とするため，現実的ではありません. そのために，倍精度浮動小数点数と呼ばれる有限の桁に近似します. さらに，もっと簡単な十進数の0.1も，コンピュータが得意とする2進数では無限の桁を持つため，コンピュータで直接的に扱うことは難しくなります. たった，0.1という単純な数でさえも近似で値である倍精度浮動小数点数でコンピュータは保持します. その上で，倍精度浮動小数点数で持っている値に対する演算(例えば，0.1 + 0.01)も，また，倍精度浮動小数点数で表せない場合は，近似しなければなりません. スーパーコンピュータで「100万次元の問題が解けた!」といっても，ものすごい膨大な近似の計算(10の18乗回以上の近似計算?)を行って，「解けた!」というのは本当に正しい結果なのでしょうか?

そこで，研究テーマである精度保証付き数値計算が活躍します. 精度保証付き数値計算では，計算機で計算する上で発生する全ての誤差を把握し，「得られた近似解」の周辺に「元の法則に従って問題の真の答え」があることを，コンピュータを用いて証明します. すなわち，「得られた近似解の品質を保証する手法」です.

例えば，拡散項付きのロトカ・ボルテラ方程式(捕食者と被捕食者のモデル)のDirichlet境界値問題を考えてみましょう: \[ -\Delta u = a u - u^2 - cuv \] \[ -\Delta v = b v + duv - v^2 \] \[ u = v = 0 \] そのとき、\(a=100,b=7,c=100,d=-8\)と設定すると以下の図の近似解を得ることができます. 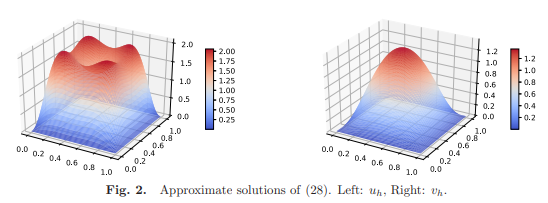Solution of Lotka-Volterra Equation この結果が本当に正しいのか?っというのが精度保証付き数値計算によって示すことができ，微分方程式の真の解と上図の近似解の差は\( 1.131 \times 10^{-11} \)以下であることを証明することができます. よって，十分小さい値であることから，非常に精度の良い近似解であることがわかりました. そもそも，上の方程式の解があるかどうか，ということすら把握することは難しい状況です. もちろん，方程式の解がなければ，近似解も何もないため，精度保証付き数値計算では，上の方程式の解の存在も証明してから，結果を保証しています. そのために，「計算機援用証明法」(コンピュータを使った数学の証明)という呼ばれ方もします. このような\( \Delta \)が現れるような偏微分方程式の解の精度保証付き数値計算法は1988年に九州大学 名誉教授である中尾 充宏 先生によって開発された日本発の技術です.
(上の例について: Kouta Sekine, Mitsuhiro T. Nakao, and Shin'ichi Oishi: "Numerical verification methods for a system of elliptic PDEs, and their software library", Nonlinear Theory and Its Applications, IEICE, Vol.12, No.1, pp.41-74, Jan., 2021.)

今までの偏微分方程式の解に対する精度保証付き数値計算法では，解が存在して，近似解の近くにあることを示す方法でした. それに対し，間違った近似(?)解が得られた場合には，「何もわからない...」ということしかできませんでした. このような問題に対しても，取り組んでおります. 例えば，鉄合金の相分離過程を表すアレン・カーン方程式 \[ -\Delta u = \lambda ( u - u^3) \] \[ u = 0 \] をコンピュータで計算してみると次のような近似(?)解を得ることができます: 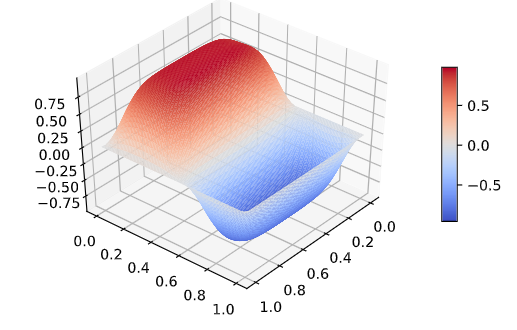Spurious solution of Allen-Cahn Equation 一見すると正しそうな解に見えます. しかし，こちらの解は偽解と呼ばれるアレン・カーン方程式の解とは全く無関係なものです. このようなダメな結果に対して，得られた結果の近くに真の解がないことを示す方法が2021年に私たちが開発しました.
(上の例について: Kouta Sekine, Mitsuhiro T. Nakao, Shin'ichi Oishi, and Masahide Kashiwagi: “A numerical proof algorithm for the non-existence of solutions to elliptic boundary value problems”, Applied Numerical Mathematics, 169, pp. 87-107, Nov., 2021.)


VCP Library

精度保証付き数値計算法は，100%の保証を与えるために，1bitたりともミスが許されません. そのために，「コンピュータの仕様」「数値計算のアルゴリズム」「精度保証付き数値計算法の仕組み」など全てを理解していないと，プログラミングすることはできず，なかなか導入が難しい分野です. この問題を解決するために，私はC++でかかれたライブラリとしてVCP Libraryを公開し，気軽に使用できるように環境を整備しています:
VCP library
Go to VCP Library
VCP Libraryでは，早稲田大学 教授 柏木雅英先生の開発したkvライブラリと組み合わせることで，真価を発揮します.


チュートリアルなどで使用した資料

半線形楕円型境界値問題の精度保証付き数値計算法の入門 ( 発表スライド )
2018年12月26日に東京大学で行った 日本応用数理学会 三部会連携「応用数理セミナー」の資料です．
楕円型偏微分方程式の解の精度保証付き数値計算法はどうやるの?というのを，一から説明しています．
精度保証付き数値計算法ではどのようにして，「不動点方程式化」や「不動点定理」を行うか説明しています．
続きは書籍で!!



Introduction to Verified Computation
2015年9月1日,4日に新潟大学で行った精度保証付き数値計算の資料です．
FortranとC言語を用いて連立一次方程式の精度保証付き数値計算法を紹介しています．
特にOpenBLASやLapackの導入方法を詳しく書きました．
(ごめんなさい．参考文献は書いていません...主に大石進一先生の精度保証付き数値計算法，IEEE754 standard)



楕円型連立半線形偏微分方程式の解に対する精度保証付き数値計算法
2014年12月26日に早稲田大学で行った 日本応用数理学会 三部会連携「応用数理セミナー」の資料です．
連立楕円型偏微分方程式の精度保証付き数値計算法を紹介しています．
特に線形化作用素の逆作用素のノルム評価について詳しく書きました．
また，さりげなくシグマノルムを導入しています．．